Mathematics trigonometry DO THIS & TRY THIS Sums Solutions
DO THIS
1. Identify "Hypotenuse", "Opposite side" and "Adjacent side" for the given triangles
Sol. ln the triangle PQR
Opposite side =PQ
Hypotenuse = PR
2.1) for angle X
2) For angle Y
Sol. In the triangle XYZ
1) För angle XOpposite side = YZ
Adjacent side= XZ
Hypotenuse= XY
Opposite side =XZ
Adjacent side =YZ
Hypotenuse = XY
Also Check
Introduction to Knowing Our Numbers Key Points
SSC (10th class) Trigonometry Exercise - 11.1 Solution
SSC(10th class) Trigonometry Exercise - 11.1 Solutions
3. In triangle XYZ, angle Y is right angle, XY=17 cm and YZ=15 cm, then find (i) sin X (ii) cos Z. (iil )tanX
Sol: Given triangle XYZ,
∠Y is right angle.
By Pythagoras theorem
XZ 2 = YZ 2 +XY 2
XY 2 = 172-152
XY 2 =
289-225
XY 2 = 64
XY = √64
XY = 8
i) sin X = opposite side to ∠x / Hypotenuse
= YZ / XZ=15/17
= YZ / XZ=15/17
= YZ/XZ=15/ 8
TRY THIS:
1. Write length of "Hypotenuse", "Opposite side" and "Adjacent side" for the given angles in the given triangles.
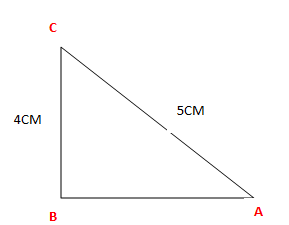
ii) For angle A
(5)2 = AB 2 +42
25 =AB2+16
AB 2 = 25 –16
AB 2 =9
AB = V 9
AB =
3
Opposite side = AB = 3 cm
Adjacent side = BC = 4 cm
Hypotenuse = AC = 5 cm
Opposite side = BC = 4
cm
Adjacent side =AB = 3
cm
Hypotenuse AC = 5 cm
Given that
BC+CA = 23……... (1)
BC-CA =7………. .(2)
Solve equation 1 and 2
BC+CA = 23……... (1)
BC-CA =7………. .(2)
................................
Add 2 BC = 30
BC = 30/2
BC =15
Substituting BC =15 in equation (1)
BC + CA = 23
CA = 23 – BC
CA = 23 - 15
CA = 8
By Pythagoras theorem
AB 2 =
AC 2 + BC 2
= 82 +152
= 64+22
AB 2= 289
AB =√ 289
=√17 X 17
=17
sin A =BC/AB = 15/17
tan B = AC/BC= 8/ 15

















0 comments:
Post a Comment