Mathematics trigonometry Exercise - 11.1
 |
| Mathematics Trigonometry Exercise |
6. If ∠a and ∠x are acute
angles such that Cos A = Cos X then
such that ∠a = ∠x
Sol: Given that Cos A = Cos X ------ (1)
We
have Cos A =AB/AC and Cos X = XY /XY
AB/AC = XY/XZ From Eg (1)
AB/AC =
XY/XZ = k ------ (2)
From ⧍ABC
BC 2 =AC 2-AB 2
BC 2
= AC 2 - (k AC) 2
BC 2=AC
2 - k 2 AC 2
BC 2=AC 2 (1- k 2)
BC =√ AC 2 (1- k 2)
BC
=√ AC 2 (1- k 2)
BC
= AC √ (1- k 2)
YZ 2
=AC 2-XY 2
YZ
2 = XZ 2 - (k XZ) 2
YZ
2= XZ 2 - k 2 XZ 2
YZ
2= XZ 2 (1- k 2)
YZ
=√ XZ
2 (1- k 2)
YZ
= XZ
√ (1- k 2)
BC/ YZ
= AC √ (1- k 2)/ XZ √ (1- k 2)
BC/ YZ
= AC/ XZ ------ (3)
From
(2) & (3) Equations
Hence AB/XY= BC/ YZ = AC/ XZ
⧍ ABC ~
⧍ XYZ ( . ̇. ∠A =∠X
)
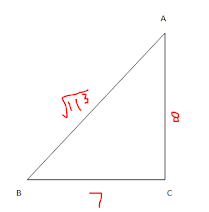
7. Cot 𝜽
=7/8, evaluate (1) (1+sin 𝜽) (1-sin 𝜽) / (1+cos 𝜽)
(1-cos 𝜽) (2) (1+sin 𝜽)/ Cos 𝜽
Sol: Cot 𝜽 =7/8
From ⧍ABC
AB 2=
BC 2+AC 2
AB 2= 72+82
AB 2=
49+64
AB 2=113
AB =√113
2)(1+sin 𝜽) (1-sin 𝜽) /(1+cos 𝜽) (1-cos 𝜽)
= 1-sin 2 𝜽/1-cos 2
𝜽
= cos 2
𝜽 /sin 2 𝜽
= Cot 2
𝜽
= (BC/AB) 2
= (7/√113)
2
= 72/(√113) 2
=49/113
(2)(1+sin
𝜽)/ Cos 𝜽
=1/Cos 𝜽+Sin
𝜽/Cos 𝜽
=Sec 𝜽+Tan
𝜽
=AB/BC+AC/BC
=√113/
7+8/7
=√113+8/7
8. In a Right angle triangle ABC, Right angle is at B, Tan A =√3 then find the value of 1) Sin A Cos C + Cos A Sin C 2) Cos A Cos C - Sin A Sin C
Sol: Given that Tan A = √3/1
(Hypotenuse)
2= (side) 2+ (side) 2
(Hypotenuse) 2= (√3) 2 +1
=3+1
=4
1 1) Sin A Cos C + Cos A Sin C
=√3/2 ×√3/2+1/2×1/2
=3/4 +1/4
=4/4
=1
2) Cos
A Cos C - Sin A Sin C
=1/2×√3/2 - 1/2×√3/2
=√3/4 -√3/4
=0














Trigonometry equations are always difficult to solve. Because you cannot learn and perform these types of equations in the first attempt. Doing it over and over again is the only way to learn trigonometry. Since childhood, trigonometry was the only subject that intimidated me when I appeared for the exam. But with the help of a lot of practice now it has become easier for me. I have learned trigonometry from online tutors. For more information contact h1 math tuition.
ReplyDelete