Introduction To Trigonometry | Trigonometry Definition,formulas,Ratios

Trigonometry Definition and formulas

Hi friends and my dear students! In this post, I have covered Introduction To Trigonometry. After Reading Trigonometry Definition,formulas, Ratios, Please do share it with your friends. You can Learn Maths for All Classes here.

Introduction To Trigonometry

Historical facts: Hipparchus of Nicaea (190 BC-120 BC). was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry but is most famous for his incidental discovery of p recession of the equinoxes. Hipparchus, credited with compiling the first trigonometric table, is known as 'the father of trigonometry' Hipparchus was the first to tabulate the corresponding values of arc and chord for a series of angles. The first use of the idea of 'sine' in the way we use it today was in the work Aryabhatiyam by Aryabhata in AD 500.

Introduction: The word "Trigonometry' is derived from three Greek words Tri-Gonia-Metron. "Tri' means 'three', 'gonia' means "an angle' and 'metron' means 'measure, In recent times trigonometry is widely applied in many branches of Science and Engineer Such as seismology, design of electrical circuits, estimating the heights of tides in the ocean

Recapitulation:

Angle:

Two rays are intersecting at one common end point is called an angle.

An angle is usual denoted by A, B. ... etc.

Units of measurements of angles:

1.The sexagesimal system :

In this system unit of measurement of an angle is 'degree', Degree : In this system one

Complete rotation is divided into 360 equal parts. Each parts is called 'a degree',

denoted as 1°. In this system, one right angle is 90°

2. Centesimal system :

In this system unit of measurement of angle is 'grade'. Grade: In this system one complete rotation is divided into 400 equal parts. Each part is called 'a grade', denoted as 1 ^g. In this system, one right angle is 100 ^g

3.The circular system :

In this system unit of measurement of an angle is 'radian'. Radian : The angle subtended by an arc of the length equal to the radius of the circle at its cent re is called one radian, denoted as 1 ^c.

Note: The formula connecting the three systems can be stated as D/90=G/100 =2c/π

Where D denotes degrees, G denotes grades and C denotes radians.

You May Also Read

Mathematics trigonometry Exercise - 11.1

Trigonometric Ratios:

The ratios of sides of a right angled triangle are called trigonometric ratios of angles.

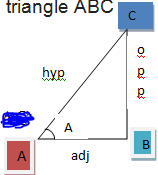
Let ABC be a right angled triangle with right angle at B and angle A is an acute angle.

In a right triangle ABC, the side BC faces the angle A is called opposite side to the angle A,

the side AB is the adjacent side to angle A and AC is the hypotenuse of  triangle ABC

1. Sin A =      side opposite to angle A / hypotenuse =BC/AC

2. cosine A = cos A = side adjacent to angle A / hypotenuse=AB/ AC

3. tangent A= tan A=side opposite to angle A /side adjacent to angle A=BC/AB

4. cosecant A =1/sin A= hypotenuse / side opposite to angle A =AC/BC

5. Secant A=1/Cas A= hypotenuse /side adjacent to angle A =AC/AB

6. cotangent A = 1/tan A=side adjacent to angle A/side opposite to angle A=AB/BC

Note: We have six trigonometric ratios and the reciprocal relations between them are as below

1) sin A x cosec A=1=>  cosec A =1/sin A  ;  Sin A= 1/cosec A

2) cos A x sec A=1  =>    sec A = 1/cos A ; cos A = 1/sec A .

3) tan A x cot A= 1 =>   cot A = 1/tan A  ;  tan A=1/cot A

• Quotient relation:

 1. tan A = sin A/cas A= sec A / cosec A

 2. cot A = cas  A/sin A= cosec A / sec A