Andhra pradesh SSC(10th class) Mathematics trigonometry Exercise - 11.1 Solutions

Mathematics trigonometry Exercise - 11.1

Hi friends and my dear students! In this post, I have covered Andhra Pradesh SSC(10th class) Mathematics trigonometry Exercise - 11.1 Solutions. After Reading Mathematics trigonometry Exercise, Please do share it with your friends. You can Learn Maths for All Classes here.

1. In right angle triangle ABC, 8 cm, 15 cm and 17 cm are the lengths of AB,BC and CA respectively. Then, find out sin A, Cos A, and tan A.        

Sol: Given in right angle triangle ABC, 8 Cm, 15 Cm and 17 Cm are the length of AB, BC and CA respectively  

 i) sin A= Opposite side /Hyptenuse =BC/AC=15/17

 ii) Cos A = Adjacent side/Hyptenuse = AB/AC =8/17

 iii) Tan A =Opposite side/Adjacent side=BC/AB=15/8

 2. The sides of a Right angle triangle PQR are PQ = 7 cm, QR = 24 cm and √Q = 90 respectively. Then find, tan P, tan R.

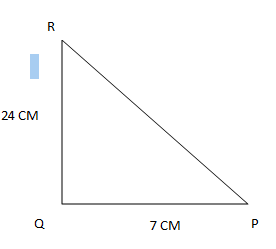
Sol:  Given the sides of a right angle triangle PQR are PQ = 7 cm, QR = 24 cm and ∠Q=90 

BY Pythagoras theorem

 PR ² = PQ ²+ QR ²                 

PR ²= (7) ²+ (25) ²

PR ²= 49+ 576

PR ²= 625

PR =√625

PR =25

Tan p= QR/QP=24/7

Tan R= QP/QR=7/24

Tan p -Tan R = 24/7 - 7/24

                     =  24 × 24 - 7 × 7

                        -----------------

                              168

                    = 527/168

Read More

Introduction To Trigonometry

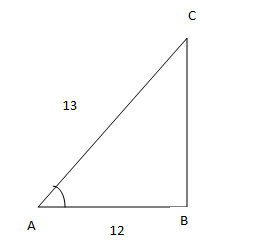
3. In a right angle triangle ABC with right angle at B, in which a= 24 units, b = 25 units and∠BAC =Ø Then, find CosØ and tanØ.

 Sol: Given in a right angle triangle ABC with right angle at B, in which 

 a = 24 units, b= 25 units and ∠BAC=Ø  

 BY Pythagoras theorem

 AC ² = BC ²+ AB ²

(25) ²= (24) ²+ (AB) ²                               

625 = 576 + (AB) ²

(AB) ²= 625-576

 (AB) ² =49

(AB)  = √49

 AB = 7

 I ) Cos Ø= AB/AC = 7/ 25

ii) Tan Ø =BC/AB = 24/7

 4. If Cos A =12/13 than find sin A tan A.

Sol: Given Cos A = Adjacent side/Hypotenuse=12/13

BY Pythagoras theorem

AC ² = BC ² + AB ²

13 2 =12 2+ BC ²

BC ² =13 2-12 2                               

BC ² =169-144

BC=√25

BC=√5×5

BC=5

Now   

Sin A = BC/AC =5/13

Tan A = BC/AB =5/12

 5. If 3 tan A = 4 than find sin A Cos A

 Sol: Given tan A = Opposite side/Adjacent side= 4/3

BY Pythagoras theorem

AC ²= AB ² + BC ²

AC ²= 32+42

AC ²=9+16                       

AC ²=25

AC=√25

AC=5

Now    Sin A = BC/AC =4/5

           Cos A = AC/AB =3/5